Computing a Fibonacci number

This tutorial shows you how to create a distributed version of the classic doubly recursive Fibonacci number computation using Jicos. Although this computation is not inherently interesting, it is an extremely light-weight example of a recursive computation that can be done in parallel usng Jicos. Due to its small computational load, this computation stresses any asynchronous parallel computing system because of the large amount of synchronization it requires: It is a computation that is essentially all overhead. Most importantly, it is a simple computation, allowing us to focus on the Jicos API.

Before we dive into the Jicos aspects of the problem, let's review this simple computation. We can define the nth Fibonacci number recursively as follows:

  • f(n) = 1, for n = 0 and 1;
  • f(n) = f( n - 1 ) + f( n - 2 ), for n > 1.
This definition forms the basis of a direct doubly recursive implementation. In the definition above, the computation proceeds by first decomposing the computation of the nth Fibonacci number into successively smaller Fibonacci number computations until the smaller computations satisfy the conditions of the base case (n = 0 or 1). The results from the base case are then added to produce the Fibonacci number for n = 2. The Fibonacci numbers for 1 and 2 are then used to form the 3rd Fibonacci number. This composition process proceeds until the initial number is computed. An illustration of this process for the 4th Fibonacci number is given below as a directed acyclic graph (dag) of tasks.

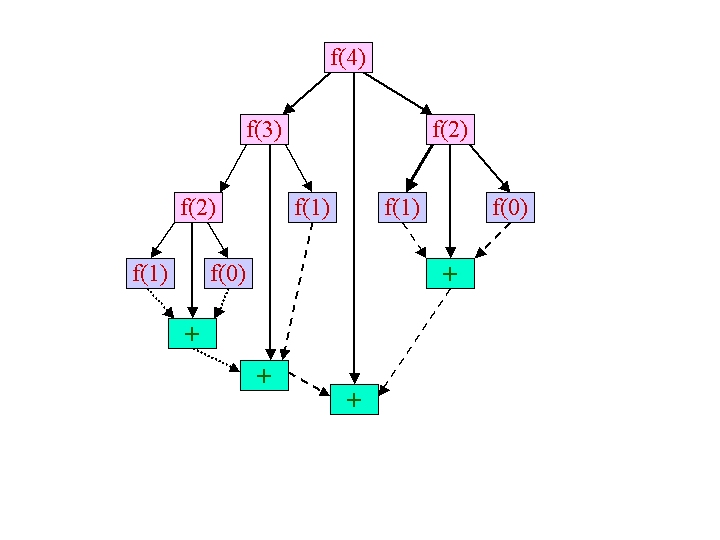To render the task dag as a parallel program in Jicos, we first identify the tasks that we want done in parallel. In this example, we identify each node of the dag above with a task. Any 2 tasks that do not lie on the same directed path can, in principle, be done in parallel. We could create 3 kinds of tasks: a decompose task, a base computation task, and a compose task. In this example, we use only 2 task types: F and AddInteger. The F task incorporates both the decompose and base tasks. Looking at the task graph above, we see that the F task takes 1 input, input[0], and either creates 3 subtasks xor computes 1 output (only if it is a base computation). AddInteger returns the sum of its inputs.

The Classes

Now, let's look at actual Java classes. An explanation of the class definition follows.

Application

After registration is complete, the application:
  1. parses the number supplied as args[1] from the command line into an int, representing the Fibonacci to compute (e.g., we pass it 5, if we want the 5th Fibonacci number).
  2. constructs the root task of the computation, an F task.
  3. invokes Hsp's compute method to deposit this root task into the Hsp. 
  4. The application then immediately invokes getResult to obtain the Result. This is a blocking call: it returns only after the Hsp obtains a result. The application then gets the value of that Result with Result's getValue method.

F

  • The constructor takes an int representing the number to compute. If we are computing the nth Fibonacci number, we invoke the constructor with an argument of  n. The returned value of a root task is not sent to a successor task; there is no successor task. It is returned to the application program as the value of a getResult method invocation.
  • The execute method does exactly 1 of 2 things, depending on the value of n:
    • returns 1, if 0 < n < 2.
    • decomposes the computation into 2 sub-computations, F( n - 1) and F( n - 2 ). They must be dispatched via the compute method. The values resulting from these tasks are the inputs of a compositional task, AddInteger, whose returned value is F( n ) =  F( n - 1) + F( n - 2 ).

AddInteger

This is a Task that is part of the jicos.services.tasks package that is included in the Jicos download. Its execute method simply returns the sum of its inputs. In this application, there always are 2 inputs.

These 3 classes, Application, F, and AddInteger are all that we need.

The output should look like this:

F( 5 ) = 8

where 5 is an example of what you specified as args[1], and 8 is its Fibonacci number.