CS170 The Threaded Matrix Multiply Lab

Synopsis

The assignment is to create a threaded program that computes the matrix product of two matrices that are presented to it as text files in a given format. Both the correctness and the speed-up of the program (due to parallelism) will be considered as well as the degree to which the program handles error conditions. The program must conform to a specific prototype and generate output in the specified format.

Goals

The goals for this lab are With that in mind, it is designed as a warm up exercise. If you find yourself struggling with any part of this lab, please seek help from the instructor and/or the TAs. In particular, the remaining programming assignments in this class assume that this assignment does not exceed your C programming skills. If it does, then you should consider it a sign that you need to brush up on your C. We can help but you need to be proactive about seeking that help.

The Blue Pill or the Red Pill?

If you haven't seen it in a while, a matrix is a rectangular array of numbers. Each element in the array can be identified by its row and column number.

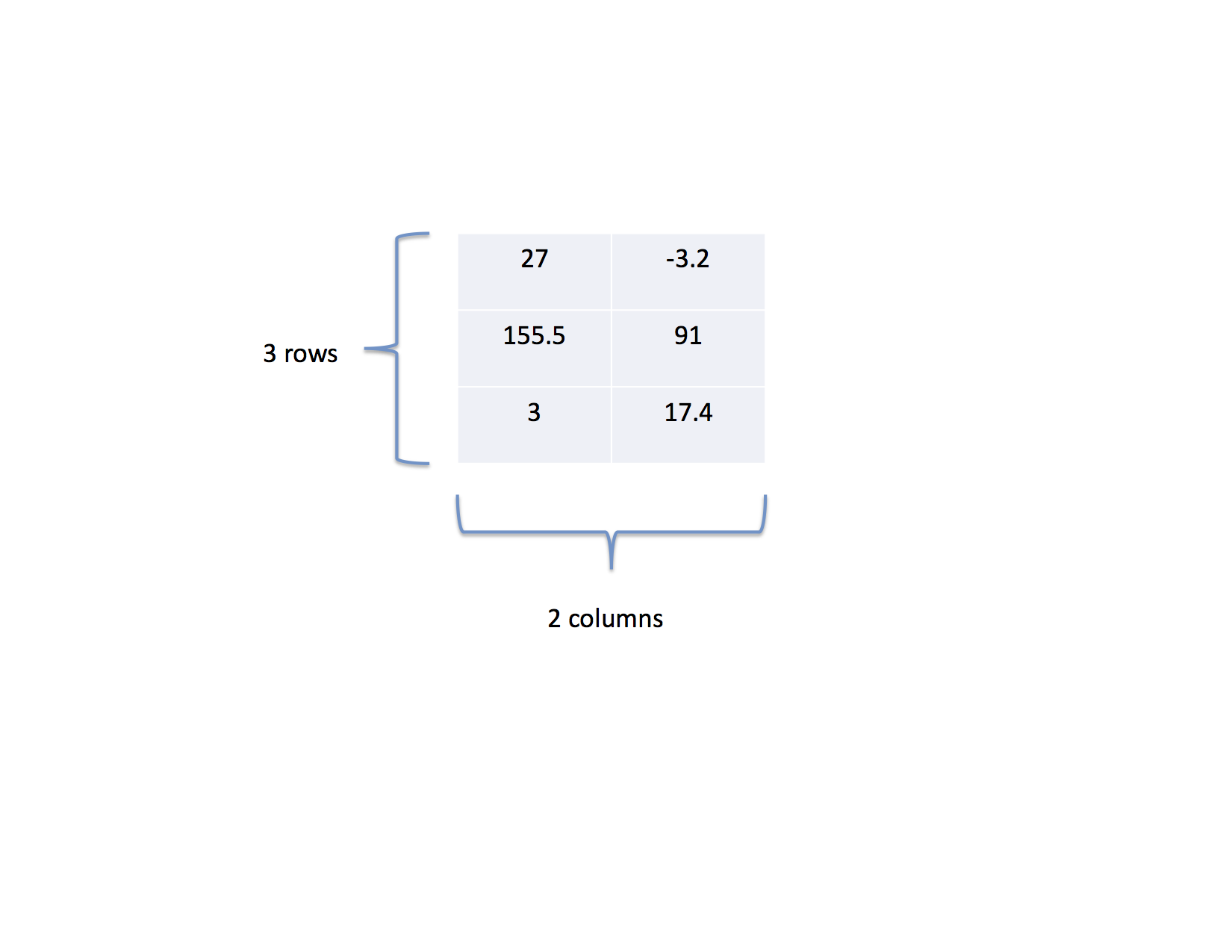
For example, the following matrix has 3 rows and 2 columns

In this class, we'll use "zero" as the first counting number (as computer scientists are sometimes prone to doing) thus the element located at the "zeroth" row and "zeroth" column is the number 27. Similarly, the element in the second row, first column is 155.5. Notice the slight disparity between English and the counting numbers here. We'll try to be precise but the concept of locating an element in a matrix is what is important so as long as you understand that each element is uniquely named (addressed) by its row number and its column number you have it.

In that light, we will use the "convention" that matrix elements are named by an ordered pair, where the first entry in the pair is the row number and the second is the column number. Using this notation 

element (0,0) is 27
element (0,1) is -3.2
element (1,0) is 155.5
element (1,1) is 91
element (2,0) is 3
element (2,1) is 17.4
Notice that there are six elements in total which is the number of rows multiplied by the number of columns.

Row Major Order

The process of listing out the contents of an array sequentially turns out to be important when writing programs that manipulate matrices (as you will do in this assignment). The convention we will use (and the convention used in most C programs) is to list them by row -- called row major order. That is you list all of the elements in the zeroth row, then the elements in the 1st row and so on. In this example, there are three rows -- zero one and two -- and the elements of the zeroth row are all listed before the elements of the first row.

Additionally, within each row, elements are listed from lowest column number to highest. Thus, for the zeroth row, the elements are listed column 0 and then column 1.

This convention is not enforced by C and indeed other languages (like Fortran) use a different convention. However some convention is necessary so that it is possible to write programs that simply treat matrices as first-class objects.

For C, this latter requirement is especially important because the language only includes the ability to store values in a one-dimensional array. Notice that any two dimensional matrix having M rows and N columns can be stored in a one-dimensional array with M * N elements. Further, using row major order, they are stored in the array in the order shown.

Confused? Consider the following C programming example: 

#include < stdio.h >
int main(int argc, char **argv)
{
	double one_dim_array[6];
	int i;
	int j;

	one_dim_array[0] = 27;     /* (0,0) */
	one_dim_array[1] = -3.2;   /* (0,1) */
	one_dim_array[2] = 155.5;  /* (1,0) */
	one_dim_array[3] = 91;     /* (1,1) */
	one_dim_array[4] = 3;      /* (2,0) */
	one_dim_array[5] = 17.4;   /* (2,1) */

	for(i=0; i < 3; i++) {
		for(j=0; j < 2; j++) {
			printf("element (%d,%d): %f ",
				i,j,
				one_dim_array[i*2+j]);
		}
		printf("\n");
	}

	return(0);
}
What does it do? Try compiling and running it. You should get something like 
element (0,0): 27.000000 element (0,1): -3.200000 
element (1,0): 155.500000 element (1,1): 91.000000 
element (2,0): 3.000000 element (2,1): 17.400000
Look familiar? If it does, then notice how the loops run. The outer loop is counting off rows in the index i while the inner loop indexes columns in the j variable. Beacuse the data is stored in row-major order in the one_dim_array array, it can be indexed (using i and ) as 
one_dim_array[i*2+j]
which is generally true. That is, if cols is the number of columns, then 
array[i*cols+j]
accesses the (i,j) element in a one-dimensional array storing a matrix in row-major order. Take a minute to figure this out for yourself. It will help in the future. Basically, to get to the (i,j) element in the one-dimensional array you need to go past i rows, each of which contains cols elements and then index j more elements in to get to (i,j). In this example, cols is 2 so array[i*2+j] yields the (i,j) element.

Matrix Multiply

Now that you have -- uh -- mastered the matrix (ouch), you can think about matrix arithmetic. Two matraces can be added and subtracted (each element solution is just the sum or difference of the corresponding elements in the two matraces being added or subtracted). They also can be multiplied, but the multiplication process is somewhat non-intuitive.

Specifically, each element (i,j) of the product of two matraces is the pairwise sum of the products of the elements i_th row in the first of the two matraces being multiplied and the j_th column of the second matrix.

What?

Try it this way. In the matrix product 

C = A * B
where A and B are matraces, the elements (i,j) of the C matrix are 
C(i,j) = sum of each value of the i_th row of A times the corresponding value
of j_th column of B
Notice the slightly new notaion. We'll use X(i,j) to denote the (i,j) element of the matrix X.

Probably the easiest way to see how this works is through an example. Consider the two matraces A and B in the following figure:

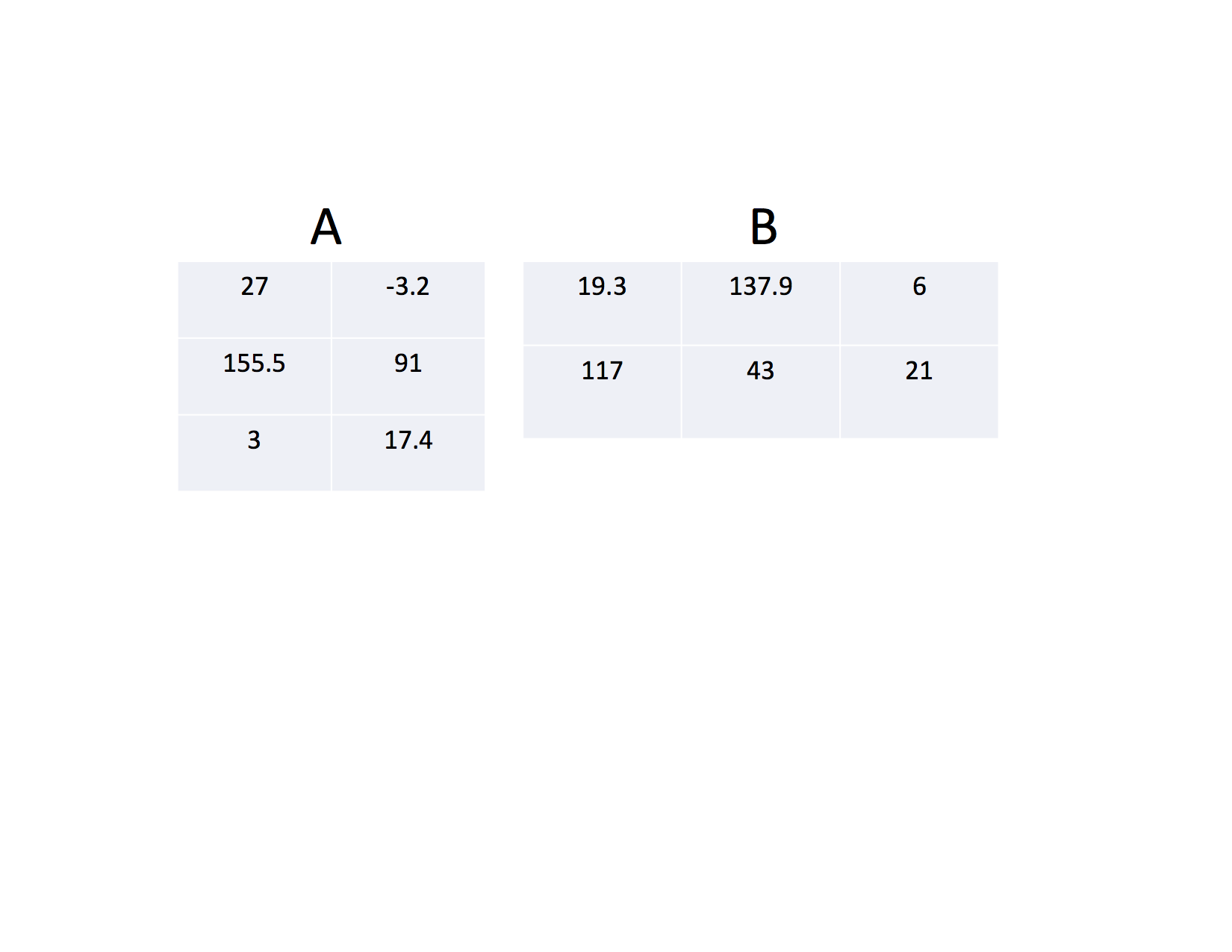
What is the (0,0) element of the resulting product matrix C? It is computed as 
C(0,0) = A(0,0)*B(0,0) + A(0,1)*B(1,0)
The elements of the zeroth row of the A matrix are paired up with the zeroth column of the B matrix and multiplied. C(i,j) is then the sum of these multiplications. Thus 
C(0,0) = 27*19.3 + (-3.2)*117
or C(0,0) = 146.7. Notice that multiplication takes precedence over the addition.

Similarly 

C(1,0) = A(1,0)*B(0,0) + A(1,1)*B(1,0)
or 
C(1,0) = 155*19.3 + 91*117
which is 13638.5. Again, the algorithm walks along the i_th row of the j_th column of the B matrix. In this last example, it pairs up elements from row 1 of the A matrix and column 0 of the B matrix.

Thus, C = A * B is 

	146.700000 3585.700000 94.800000
	13648.150000 25356.450000 2844.000000
	2093.700000 1161.900000 383.400000

Ensuring Correctness

If it hasn't occurred to you yet, matrix multiplication is a little bit more restricted in terms of what can be multiplied than its scalar counterpart. For example, it doesn't necessarily commute. That is, A * B is not automatically equal to B * A. Why? Notice that he product of A * B has as many rows as A and as many columns as B. If A is a 3 x 2 matrix and B is a 2 x 3, A * B is a 3 x 3 matrix but B * A is a 2 x 2 matrix. Worse, if A is a 4 x 2 matrix and B is 2 x 3, A * B is a 4 x 3 matrix but B * A is not defined. That is, for two matraces to be multiplied, the number of columns on the left hand side of the multiplication symbol must be equal to the number of rows of the matrix on the right hand side of the multiply symbol or they don't multiply at all. Scalars don't have this set of restrictions. It is always possible to multiply two scalars and the "side" of the multiply symbol doesn't matter.

Thus your code will need to make sure that the multiplication of two matraces is defined and also be careful about how big the result will need to be.

The Assignment: Threading Matrix Multiply

In this assignment you you are to write a version of matrix multiply that uses threads to divide up the work necessary to compute the product of two matraces. There are several ways to improve the performance using threads. For this class, you only need to divide the production row dimension among multiple threads in the computation. That is, if you are computing A * B and A is a 10 x 10 matrix and B is a 10 x 10 matrix, your code should use threads to divide up the computation of the 10 rows of the product which is a 10 x 10 matrix. If you were to use 5 threads, then rows 0 and 1 of the product would be computed by thread 0, rows 2 and 3 would be computed by thread 1,...and rows 8 and 9 would be computed by thread 4 (as depicted in the following graph).

If the product matrix had 100 rows, then each "strip" of the matrix would have 20 rows for its thread to compute. This form of parallelization is called a "strip" decomposition of the matrix since the effect of partitioning one dimension only is to assign a "strip" of the matrix to each thread for computation.

Note that the number of threads may not divide the number of rows evenly. For example, of the product matrix has 20 rows and you are using 3 threads, some threads will need to compute more rows than others. In a good strip decomposition, the "extra" rows are spread as evenly as possible among the threads. For example, with 20 rows and 3 threads, there are two "extra" rows (20 mod 3 is 2). A good solution will not give both of the extra rows to one thread but, instead, will assign 7 rows to one thread, 7 rows to another, and 6 to the last.

Note that for this assignment you can pass all of the A and B matrix to each thread.

Full Credit

Your program must conform to the following prototype: 
my_matrix_multiply -a a_matrix_file.txt -b b_matrix_file.txt -t thread_count
where the -a and -b parameters specify input files containing matracies and thread_count is the number of threads to use in your strip decompostion.

The input matrix files are text files having the following format. The first line contains two integers: rows columns. Then each line is an element in row major order. Lines that begin with "#" should be considered comments and should be ignored. Here is an example matrix file 

3 2
# Row 0
0.711306
0.890967
# Row 1
0.345199
0.380204
# Row 2
0.276921
0.026524
This matrix has 3 rows an 2 columns and contains comment lines showing row boundaries in the row-major ordering.

Your assignment will be graded using a program that generates random matraces in this format. It can be found at http://www.cs.ucsb.edu/~rich/class/cs170/labs/mmult/print-rand-matrix.c. You will need to write a funtion that can read matrix files in this format and to do the argument parsing necessary so that the prototype shown above works properly.

Your program will need to print out the result of A * B where A is contained in the file passed via the -a parameter and B is contained in the file passed via the -b parameter. It must print the product in the same format (with comments indicating rows) as the input matrix files: rows and columns on the first line, each element in row-major order on a separate line.

Put another way, when your assignment is graded, it will be executed using the prototype shown above using the file format shown and the results compared (electronically) to that generated by a known working solution. Part of the assignment is to ensure that your C coding skills are sufficient to accomplish this task.

Your solution will also be timed. If you have implemented the threading correctly you should expect to see quite a bit of speed-up when the machine you are using has multiple processors. For example, on my laptop 

my_matrix_multiply -a a1000.txt -b b1000.txt -t 1
completes in 8.8 seconds when a1000.txt and b1000.txt are both 1000 x 1000 matracies. When I run 
my_matrix_multiply -a a1000.txt -b b1000.txt -t 2
the time drops to 4.9 seconds (where both of these times come from the "real" number in the Linux time command).

Note this method of timing includes the time necessary to read in both A and B matrix files. For smaller products, this I/O time may dominate the total execution time. So that you can time the matrix multiply itself during development, I've provided a C function that returns Linux epoch as a double (including fractions of a second). This function is available from http://www.cs.ucsb.edu/~rich/class/cs170/labs/mmult/c-timer.c You are free to use it during development to time different parts of your implementation. For example, using this timing code, the same execution as shown above completes in 7.9 seconds with one thread, and 4.1 seconds with two threads. Thus the I/O (and any argument parsing, etc.) takes approximately 0.8 seconds for the two input matracies.

Please test your code thoroughly. For example, do not assume that it will always be called using square matracies, or matracies that result in a defined product. You should print a suitable error message and have your program exit if the product is undefined or if the input matrix files do not conform to the format specified. Handling error cases is part of the assignment so please make sure you code does so.

Extra Credit

Because of cache line size limitations, it may be more efficient to divide the production of the product into tesselating rectangles rather than strips. That is, each thread gets its own rectangular region and the entire product matrix is covered by all of the rectangles. Put another way, you can partition both the row dimension and the column dimension so that less of the per processor cache gets used in the production of the product. For extra credit, implement rectangular partitioning where both dimensions are partitioned.

No extra credit will be given for a solution that does rectangualr partitioning but does not conform to the prototype shown above for row-wise partitioning only. That is, do not implement rectangular partitioning and then turn in a solution that sets the column partitioning to use no threads unless your full credit solution meets the criteria described in the section above on Full Credit. If in doubt please speak to the TAs or the instructor for clarification.