Paul lived for mathematics.
While he was a genius and had a tremendous capacity for collaborating (he'd literally flit from problem to problem "helping" other mathematicians with their work), he had a knack for posing extremely simple problems that defy mathematical solution. The purpose of this lecture is to introduce you to one of them called The Party Problem.
We'll begin by illustrating The Party Problem with an example. Imagine that you are throwing a party.
You have to get your head around what the question is actually asking, before we can go further. Say you invite 15 people and you can invite anyone form the world's population. Surely you can invite 15 strangers or 15 mutual friends since you are free to pick anyone. The question is,
Is it possible to invite a set of people so that there is NOT a group of three complete strangers and there is NOT a group of three mutual friends?
If you can make the invitations such that both of these NOTs are true, then you know that the smallest number referred to in the question is at least 15.
More formally, the question can be stated thus:
You can and should bend your brain around the English language statements of the problem, which sound to me like those brain teaser puzzles in Reader's Digest, or you can resort of graph theory for a picture. Let's define a node to be a person, and an edge to represent the property of acquaintance between two people represented by nodes at the ends. Notice that, for any group of people (nodes) there are edges connecting them pairwise since two people either know each other or do not know each other. That is, the graph is fully connected. We'll further stipulate that the relationship is symmetric: if I know you, you know me. The graph is, therefore, undirected. Another term for such a graph is clique.
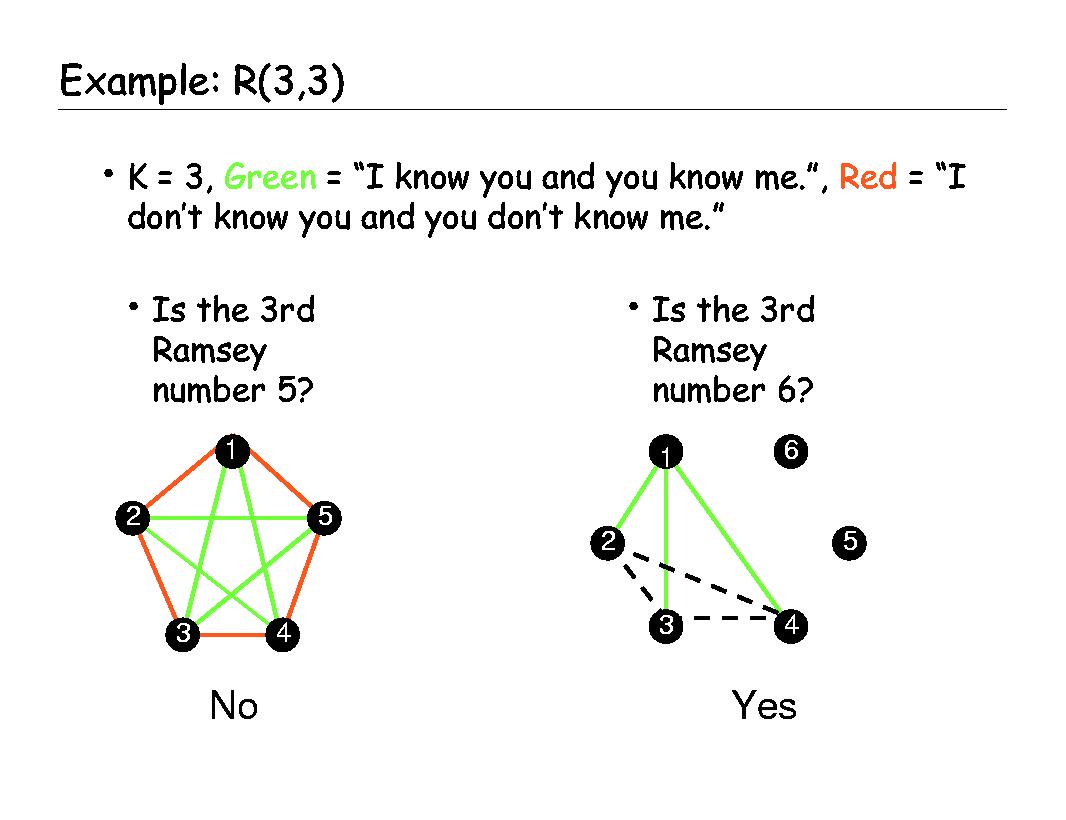
Further, we can color the edges so that they signify the binary acquaintance relationship. We'll let red indicate that the people (nodes) at the ends of an edge are strangers, and green indicate that they are acquainted. The party question for these five nodes can be restated as
Is it possible color the edges of this 5-clique such that there is no subclique of size 3 in which all of the edges in the subclique are the same color?
If the answer to this question is "yes" then you know that the 3rd symmetric Ramsey number R(3,3) is bigger than 5. Why? Because if such a coloring exists, then it is conceivable that there are 5 people who could be invited, there would be no group of 3 complete strangers (which would be signified by a red subclique of size 3) and no group of 3 mutual friends (which would be signified by a green subclique of size 3). Therefore, the smallest number for which one or the other must be true must be bigger than 5.

On the LHS of this figure, a coloring like the one described above is depicted. Notice that it does not contain a triangle (also called a 3-clique) that is all one color. As such, R(3,3) is not 5.
Now let's ask the same question about 6. Since there are six nodes and two colors, at least three edges originating at any node must be the same color (red or green). Pick a node (1 in the example) and a color for those edges (say green). Consider the colors of the dotted edges in the figure. If any one of them is also green, then they form a green triangle with the three green edges (solid lines we said were green). If none of them can be green, then they all must be red, forming a red triangle. It is, therefore, impossible to color the edges of a complete graph on six nodes without introducing a monochromatic 3-clique. Since it is possible on 5, and not possible on 5, R(3,3) is 6.
What this means is that if you throw a party and you can invite anyone, from any time, who has ever lived, on any planet, there must be a group of three complete strangers or there must be a group of three mutual acquaintances or both. Neat, huh?
R(5,5) is currently unknown as is R(k,k) for any integer value of k greater than 4. In Math terms, this situation is called an "open problem." You should think of it as a really open problem. When Math knows the answer for 3 (it is easy), 4 (it is much harder) and does not know 5 or greater (but knows that the number must exist -- unlike Fermat's Last Theorem) you know you have just stepped into the deep end of the pool. Indeed in the book "The Man Who Loved Only Numbers," (a book about Paul Erdos) many of the mathematicians interviewed said that they believed a new kind of mathematics (as yet unseen) was necessary to attack this problem successfully. One even claimed that it would be 50 years at least, before it would come to fruition.
At present, R(5,5) is known to be between 43 and 49. I do not know how those bounds were determined, but knowing it to be one of 7 numbers and not being able to say which one is a remarkable situation in mathematics. In 1997, two friends of mine and I generated counter examples for all sizes up through 42 for R(5,5) as a diversion at SC97. Some day, we'll get serious about it. Some day soon.
Thus the bank will generate a global timestamp for computationally hard proofs-of-work. It isn't Bitcoin since there is a centralized authority (the Bank), but it is logically the same abstraction. It is believed (but it hasn't been proved) that there are 328 such "coins" to be mined. We'll discuss how their uniqueness will be determined, but before we can do that we need to talk a little about what mining might look like.
0 0 1 1 1 0 1 1 0 0 0 0 0 1 0 1 1 1 0 1 0 0 0 0 1 1 0 1 1 0 0 0 0 0 1 0 1 0 1 1 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0represents a two-color graph on 10 nodes. A "0" is a red edge and a "1" is a green edge. Notice that only elements on one side of the diagonal matter. That is because [2,6] and [6,2] mean the same thing. That is again, an edge from [2,6] is the same edge that goes from [6,2] because the graph is undirected. Also -- the entries along the diagonal do not matter since nodes are not connected to themselves by an edge.
To figure out whether this graph is a counter-example for R(5,5) or not you simply need to run a set of nested loops to count the number of monochromatic subcliques of size 5 that it has. The following routine written in C uses integers to represent node adjacency color.
int CliqueCount(int *g,int gsize)
{
int i;
int j;
int k;
int l;
int m;
int count = 0;
int sgsize = 5; /* for R(5,5) */
for(i=0;i < gsize-sgsize+1; i++)
{
for(j=i+1;j < gsize-sgsize+2; j++)
{
for(k=j+1;k < gsize-sgsize+3; k++)
{
if((g[i*gsize+j] == g[i*gsize+k]) &&
(g[i*gsize+j] == g[j*gsize+k]))
{
for(l=k+1;l < gsize-sgsize+4; l++)
{
if((g[i*gsize+j] == g[i*gsize+l]) &&
(g[i*gsize+j] == g[j*gsize+l]) &&
(g[i*gsize+j] == g[k*gsize+l]))
{
for(m=l+1;m < gsize-sgsize+5; m++)
{
if((g[i*gsize+j] == g[i*gsize+m]) &&
(g[i*gsize+j] == g[j*gsize+m]) &&
(g[i*gsize+j] == g[k*gsize+m]) &&
(g[i*gsize+j] == g[l*gsize+m]))
{
count++;
}
}
}
}
}
}
}
}
return(count);
}
This routine takes 2 arguments:
Your job will be to find graphs where the dimension is 42 and the counts is 0. Only counter examples of size 42 will be considered valuable in this class.
For example, the graph on 10 nodes shown above is a counter example on R(5,5). That is, the number of single-color subcliques of size 5 in this graph is 0. However, because it is size 10 and not size 42 it isn't a "coin" from the perspective of this class.
However, not all counter examples on n nodes are embedded in a counter example on n+1 nodes. Some are, but some are not.
None the less, one startegy to consider is to try and find a counter example on a small number of nodes to start out with and then to add a node and a set of edges to make a graph one dimension bigger. If the smaller counter example is embedded in a larger one, then only the new edges need be recolored.
Another thing to realize is that the count of the number of monochromatic subcliques is a kind of "fitness function." That is, a graph with a smaller number of monochromatic subsliques is, in some sense, "better" than one with a larger number, the best being 0 subcliques. A search startegy is then
However the strategy or strategies you use are up to you. Any algorithm you wish to use is fine as long as it finds counter examples on 42 nodes.