HW1 Caches

Machines to run your code: CSIL

Exercise 1: Loop Ordering and Matrix Multiplication

To multiply two matrices, we can simply use 3 nested loops, assuming that matrices A, B, and C are all n-by-n and stored in one-dimensional column-major arrays:

for (int i = 0; i < n; i++)
    for (int j = 0; j < n; j++)
        for (int k = 0; k < n; k++)
            C[i+j*n] += A[i+k*n] * B[k+j*n];

Matrix multiplication operations are at the heart of many linear algebra algorithms, and efficient matrix multiplication is critical for many applications within the applied sciences.

In the above code, note that the loops are ordered i, j, k. If we examine the innermost loop (k), we see that it moves through B with stride 1, A with stride n and C with stride 0. To compute the matrix multiplication correctly, the loop order doesn't matter. However, the order in which we choose to access the elements of the matrices can have a large impact on performance. Caches perform better (more cache hits, fewer cache misses) when memory accesses exhibit spatial and temporal locality. Optimizing a program's memory access patterns is essential to obtaining good performance from the memory hierarchy.

Take a glance at matrixMultiply.c. You'll notice that the file contains multiple implementations of matrix multiply with 3 nested loops.

Note that the compilation command in the Makefile uses the '-O3' flag. It is important here that we use the '-O3' flag to turn on compiler optimizations. Compile and run this code with the following command, and then answer the questions below:

$ make ex2

Which ordering(s) perform the best/worst for 1000-by-1000 matrices?
How does the way this program strides through the matrices with respect to the innermost loop affect performance? Provide an analysis and explanation on the order that gives the best cr worst performance.

Exercise 2: 2D Blocking in Matrix Transposition

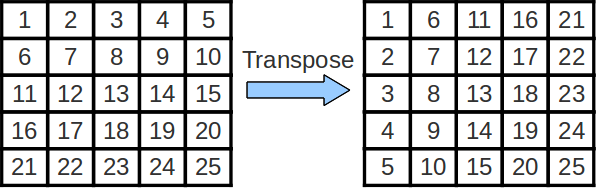
Matrix Transposition

Sometimes, we wish to swap the rows and columns of a matrix. This operation is called a "transposition" and an efficient implementation can be quite helpful while performing more complicated linear algebra operations. The transpose of matrix A is often denoted as A^T.

Cache Blocking

In the above code for matrix multiplication, note that we are striding across the entire A and B matrices to compute a single value of C. As such, we are constantly accessing new values from memory and obtain very little reuse of cached data! We can improve the amount of data reuse in the caches by implementing a technique called cache blocking. More formally, cache blocking is a technique that attempts to reduce the cache miss rate by improving the temporal and/or spatial locality of memory accesses. In the case of matrix transposition we consider 2D blocking to perform the transposition one submatrix at a time.

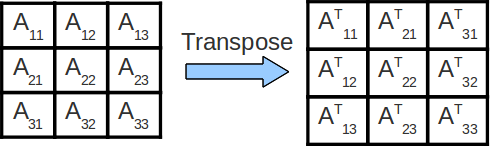
In the above image, we transpose each block A_ij of matrix A into its final location in the output matrix, one block at a time. scheme, we significantly reduce the magnitude of the working set in cache The above scheme is also called 2D loop blocking or tiling. Your task is to implement 2D blocking in the transpose_blocking() function inside transpose.c. By default, the function does nothing, so the benchmark function will report an error.

You are not allowed to change the array data structure, but can change the code structure.
Your code cannot NOT assume that the matrix width (n) is a multiple of the block size.

After you have implemented 2D blocking, you can run your code by typing:

$ make ex3
$ ./transpose <n> <blocksize>

Where n, the width of the matrix, and blocksize are parameters that you will specify. You can verify that your code is working by setting n=1000 and blocksize=33 Once your code is working, complete the following tests and give an explanation of the observed results:

Setting 1: Changing Array Sizes

Fix the blocksize to be 20, and run your code with n equal to 100, 1000, 2000, 5000, and 10000. At what point does cache blocked version of transpose become faster than the non-cache blocked version? Why does 2D blocking require the matrix to be a certain size before it outperforms the non-cache blocked code?

Setting 2: Changing Blocksize

Fix n to be 10000, and run your code with blocksize equal to 50, 100, 500, 1000, 5000. How does performance change as the blocksize increases? Why is this the case?