SIMD Intrinsics and Loop Unrolling

Machines to run your code: CSIL

Note that all code using SSE instructions work on the CSIL and Comet machines. Many newer processors support SSE intrinsics, so it is certainly possible that your machine will be sufficient, but you may not see accurate speedups.

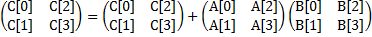
Intel hosts a variety of SIMD intrinsics, which you can find here (but these are not necessary for this assignment). The one that we're particularly interested in is the Intel Intrinsics Guide. Open this page and once there, click the checkboxes for everything that begins with "SSE" (SSE all the way to SSE4.2).

Sample SIMD Code

This sample code considers the vectorization of 2-by-2 matrix multiplication in double precision (the code we looked at in the SIMD lecture):

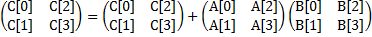
This accounts to the following arithmetic operations:

    C[0] += A[0]*B[0] + A[2]*B[1];
    C[1] += A[1]*B[0] + A[3]*B[1];
    C[2] += A[0]*B[2] + A[2]*B[3];
    C[3] += A[1]*B[2] + A[3]*B[3];

The sample code given is called sseTest.c that implements these operations in a SIMD manner.
The following intrinsics are used:

__m128d _mm_loadu_pd( double *p ) returns vector (p[0], p[1])
__m128d _mm_load1_pd( double *p ) returns vector (p[0], p[0])
__m128d _mm_add_pd( __m128d a, __m128d b ) returns vector (a0+b0, a1+b1)
__m128d _mm_mul_pd( __m128d a, __m128d b ) returns vector (a0b0, a1b1)
   void _mm_storeu_pd( double *p, __m128d a ) stores p[0]=a0, p[1]=a1

You will use the loop unrolling technique. For example, consider the supplied function sum_unrolled(): 

   static int sum_unrolled(int n, int *a)
   {
      int sum = 0;

      // unrolled loop
      for (int i = 0; i < n / 4 * 4; i += 4)
      {
         sum += a[i+0];
         sum += a[i+1];
         sum += a[i+2];
         sum += a[i+3];
      }

      // tail case
      for (int i = n / 4 * 4; i < n; i++)
      {
         sum += a[i];
      }

      return sum;
   }

Exercise 1: Writing SIMD Code

For this exercise, you will vectorize/SIMDize the following code to achieve approximately a good speedup over the naive implementation shown here: 

   static int sum_naive(int n, int *a)
   {
      int sum = 0;
      for (int i = 0; i < n; i++)
      {
         sum += a[i];
      }
      return sum;
   }

You might find the following intrinsics useful:

__m128i _mm_setzero_si128( ) returns 128-bit zero vector
__m128i _mm_loadu_si128( __m128i *p ) returns 128-bit vector stored at pointer p
__m128i _mm_add_epi32( __m128i a, __m128i b ) returns vector (a0+b0, a1+b1, a2+b2, a3+b3)
   void _mm_storeu_si128( __m128i *p, __m128i a ) stores 128-bit vector a at pointer p

Start with sum.c. Use SSE instrinsics to implement the sum_vectorized() function.

To compile your code, run the following command:

make sum
Notice that the code uses clock cycles to report the time performance and you may use command "lscpu" in a Linux machine to obtain the CPU clock frequency and adjust the parameter setting in the code.

What to submit

Exercise 2: Additional Loop Unrolling

You can obtain even more performance improvement with additional loop unrolling! Carefully unroll the SIMD vector sum code that you created in the previous exercise.

Within sum.c, copy your sum_vectorized() code into sum_vectorized_unrolled() and unroll it four times.

To compile your code, run the following command:

make sum

What to submit: