PageRank With Spark


Due March 1 before class

Update on Feb 20: add a sample Spark python link.
Update on Feb 23: clarify the submission requirement.

Goals

In this assignment, you will use the Spark programming paradigm to implement a variations of the classic PageRank algorithm. You will be transforming an input RDD of a list of edges into an output RDD of a list of nodes and their PageRank scores.

Sample Spark Python code

/home/tyang/cs240sample/spark-wc at Comet contains sample Spark programs for word counting, job submission. The Makeffile shows how to submit a job.

PageRank

PageRank is an algorithm developed by Sergey Brin and Larry Page that built the early foundation of the Google search engine. We will use a simplified version.

The intuition behind PageRank is that the web can be represented as a graph, with links between pages as directed edges. The importance or "popularity" of a page on the web can be determined by how many other pages link to it. But should every link be treated equally? A link from a popular site like Google's homepage should be more important than a link from an unpopular blog. We want to weigh links from more important pages more than edges links from less important edges when computing the PageRank score of a page. We need PageRank values to determine other PageRank values, and since all nodes depend on each other and the graph isn't necessarily acyclic, this becomes a chicken and egg problem!

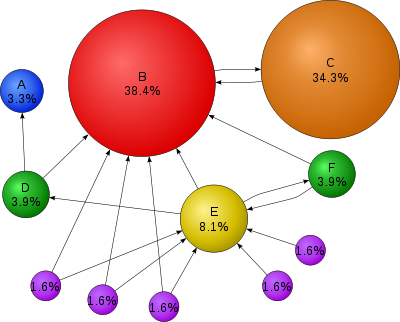
We can represent users browsing the web under a random surfer model. Sometimes the user will stay on a page, sometimes the user will click on a link and go to another page, or sometimes a user might enter a url in address bar and randomly "teleport" to any page on the web. We can then use this model to iterate through timesteps, transfering PageRank scores between nodes, until we reach convergence and the scores do not change between iterations anymore.

SimplePageRank Algortihm

We will consider a random surfer model where a user has 3 options at every timestep: stay on the page, randomly follow a link on the page, or randomly go to any page in the graph. The probabilities are as follows:

If a page does not have any outlinks, than the 0.85 chance of following a link is changed to randomly going to another page NOT including the current page.

As an example, we will show how to perform the update for one timestep. In the example graph, assume that all weights are initialized to 1.0. (The probability is just the weight / total weight, which would be 0.25 for each node)

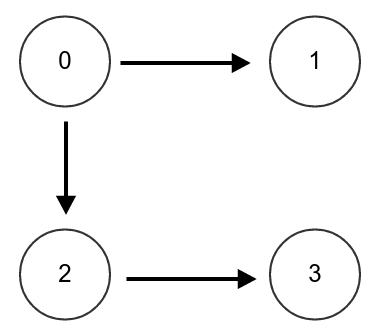
Each timestep, every node will distribute its weight to the other nodes based on the update model.

Let's calculate the contribution that node 0 gives to every other node. First, we'll take the first option. 5% of the time, we will stay on the page. So we give 5% of our weight (which is 5% of 1, or 0.05) back to the node itself. 85% of the time, we will randomly follow a link on the page. There are two links, one to 1 and one to 2, and we will follow each with a probability of 42.5%. So we give 42.5% of our weight (which is 42.5% of 1, or 0.425) to node 1 and 42.5% of our weight to node 2. Let's skip the third option for now.

Now let's do the same calculation for node 1. 5% of the time, we will stay on the page. So we give 5% of our weight (which is 5% of 1, or 0.05) to ourself. For the second option, there are no outgoing links on the page. So therefore, we will replace that option with randomly going to any node in the graph, not including itself. There are 3 other nodes in the graph. So we give 85% / 3 of our weight (which is 28.3% of 1, or .283) to nodes 0, 2 and 3.

The update for 2 and 3 can be similarly done.

Now let's think about option 3. It would be really inefficient to just add this random chance of going to any node directly, because that would make this algorithm O(V^2) in terms of the number of nodes! However, we can notice that this option is the same for every single node in the graph, it does not depend on its edges at all. For every node, we know that 10% of its weight will be distributed randomly to every node in the graph, so 10% of the sum of all the weights will be distributed randomly to every node in the graph. The sum of the weights has to be 4.0 for every iteration, so 0.4 is distributed randomly to every node, or 0.1 to each node. This is called the dampening factor.

Here is a final table of all the values we calculated. The rows represent the weights to a node, and the columns represent the weights from a contribution source.

To/From 0 1 2 3 Random Factor New Weight
0 0.05 0.283 0.0 0.283 0.10 0.716
1 0.425 0.05 0.0 0.283 0.10 0.858
2 0.425 0.283 0.05 0.283 0.10 1.141
3 0.00 0.283 0.85 0.05 0.10 1.283

Your Job

Your job is to implement the distribute_weights and collect_weights functions in pagerank/simple_page_rank.py. distribute_weights is the mapper and collect_weights is the reducer. The input for distribute_weights are tuples of the form (node, (weight, targets)) and the output of the reducer should be tuples of the same form, with updated weights from the update process. The intermediate output for the mapper should be something you decide on yourself, but make sure that the output contains ALL the information the reducer needs.

Alternatively, you can define your own structure but then you will need to change the other methods in the class. Do NOT change the method signature of either __init__ or compute_pagerank.

See the diagram for more details on how the data pipeline works.

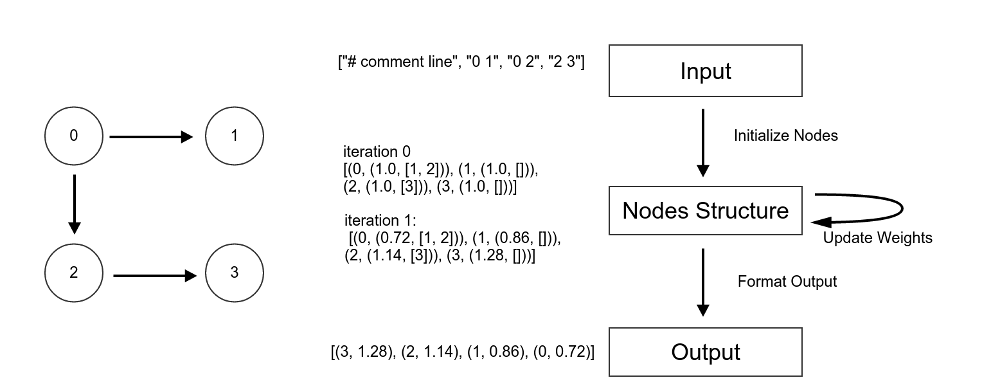You only need to add less than 20 lines of Python code in the two areas marked as "YOUR CODE HERE" in pagerank/simple_page_rank.py.

Debugging Your Program Locally under Fake RDD

You can implement and debug your code at CSIL under regular Python using a FakeRDD class that implements some of the Spark RDD interface. You may also use Comet to test your code with the Fake RDD, but there is some compatibility issue (see below on check.py).

If an RDD transformation available through Spark is not implemented in the FakeRDD class, feel free to add it yourself. Then you can use a run_mock_pagerank.py script that will run your implementation using FakeRDDs. This will help for local testing as well if you don't want to install Spark on your own computer. However, grading will be done EXCLUSIVELY using Spark and not the FakeRDD, so make sure your code works with Spark on Comet machines .

To run this local version, type: 

python run_mock_pagerank.py s [datainput] [iterations]
The input file you want to process. For example, to run 2 iterations of SimplePageRank on the data/simple1 input: 
python run_mock_pagerank.py s data/simple1 2

The test directory contains the expected results of running this simple pagerank algorithm after 1 or 20 iterations. At CSIL, you can use 

python check.py
to test 3 sample graphs with the expected results automatically. Because the Comet cluster uses Python version 2.6 which does not support some formatting features, you would have to revise check.py to match this Python 2.6 environment.

Running Your Program on Comet Machines

To run your MapReduce program through Spark at Comet, you need to use sbatch to allocate machines, set up Hadoop filesystem, and then use "spark-submit run_pagerank.py s [input] [iterations]" to run the pagerank code. This will print the output to stdout. For example, to run 2 iterations of SimplePageRank on the data/simple1 input and direct the output to a file called out, use 

spark-submit run_pagerank.py s data/simple1 2 > out

Your code also needs to pass a medium sized test using a Wikipedia dataset (called links.tsv from the tar.gz file). The links in this dataset use names instead of numbers, and a script is provided to convert between names and numbers. The processed data file with numbers representing nodes is in "data/wiki". To see the pagerank of each node with its corresponding name: 

spark-submit run_pagerank.py s data/wiki 20 > temp
python utils/map_to_names.py temp data/wiki_mapping.json > wiki_out

Your code should be linear in the number of edges, and definitely NOT quadratic in the number of nodes. The run on the wikipedia dataset for 20 iterations should not take more than 5 minutes.

Which pages have the highest weights? Does that surprise you considering what you know about the PageRank algorithm?

Submission

For electronic submission, only submit pagerank/simple_page_rank.py and output of wiki data processing (wiki_out).

For the hardcopy submission, submit the code changed in simple_page_rank.py and the output of top 5 results in wiki_out.

Additional reference